Articles
The word clouds (formed in Tagxedo,
online) serve as a visual "abstract" of
the adjacent article!
William
C.
Arlinghaus
Professor Emeritus,
Department of Mathematics and
Computer Science
Lawrence Technological
University
Southfield, Michigan
(with
figures by Sandra L.
Arlinghaus)
Tyger,
tyger, burning bright,
In
the forest of the
night;
What
immortal hand or eye,
Dare
frame thy fearful
symmetry?
William Blake
People have always been
interested in symmetry.
The fact that human bodies have
bilateral symmetry makes us
think the face we see in the
mirror is a true
reflection. The fact that
this symmetry is not perfect
makes actors and actressess
demand that they be photographed
from their 'good' sides.
Mathematicians measure symmetry
using group theory. The
set of transformations which
leaves a geometric figure
unchanged forms an object called
a 'group'.
For example, an equilateral
triangle can be rotated through
120 or 240 degrees, rotated
through an axis between a vertex
and its opposite side, or just
left alone without altering its
appearance. Thus there are
six symmetries of an equilateral
triangle, which form a symmetric
group called S3.
Graph theory studies connections
among objects. Thus, to a
graph theorist, an equilateral
triangle has the same
connections, and hence the same
symmetries, as any other
triangle. Nonetheless, it
is easier to notice the
symmetries if the geometric
representation of a graph
exhibits some of the symmetry.
There are two related but
different problems which are of
interest by themselves.
1) Given a graph, what are
its symmetries?
2) Given a group of
symmetries, what graph has a
group of symmetries isomorphic
to that group? In
particular, how small a graph
exists with that group of
symmetries?
This article concentrates on the
second part of the second
problem, in particular for the
groups of rotations of an
equilateral triangle and of a
square (cyclic groups of order 3
and 4, respectively).
Frucht has shown that any group
has a graph with that graph as
its group of symmetries (1949),
and Arlinghaus has investigated
how small these graphs can be
for finite abelian groups (1977;
1985). Much notation is
used to describe these
graphs. But this article
concentrates on 'nice' pictures
of the two groups mentioned
above (denoted Z3
and Z4, respectively).
For
Z3
, one
might start
with an equilateral
triangle, but that
is known to have six
symmetries,
including the three
extra rotations
noted above.
Eventually, one
discovers that a
graph with nine
vertices is the
smallest possible
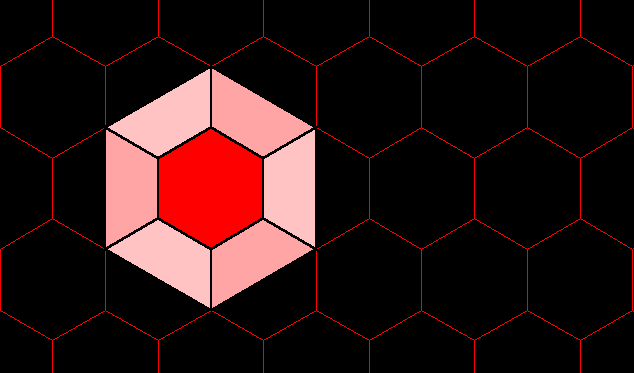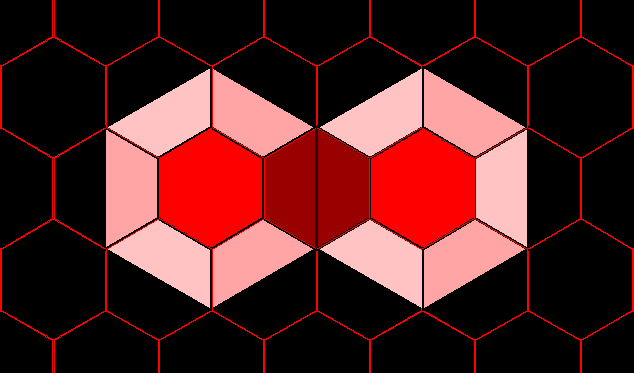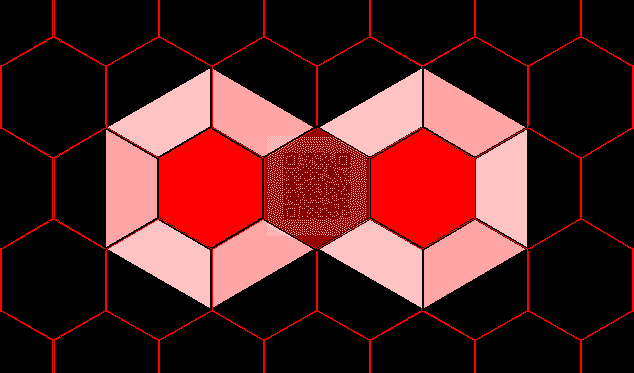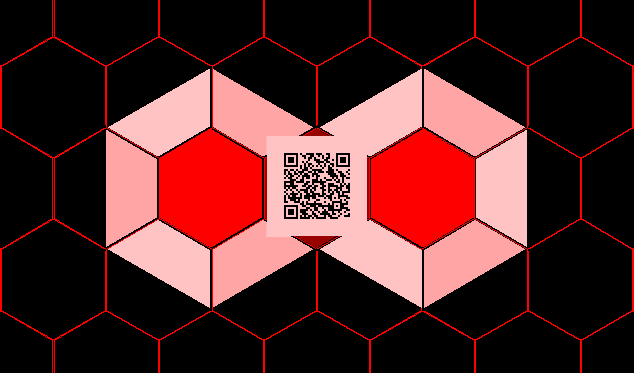
(Figure 1). It
has a picture in
which the rotations
are visible.
G
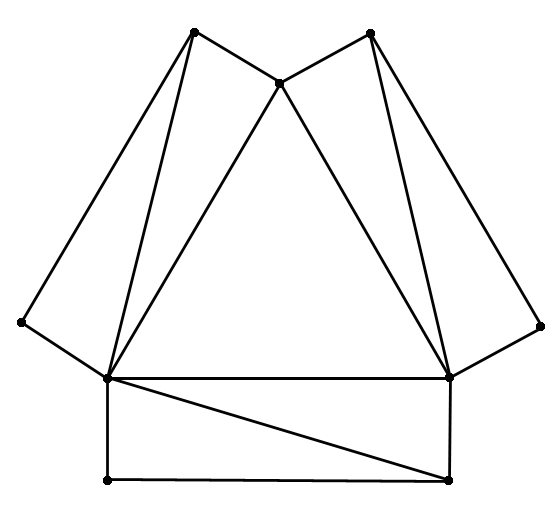
Figure 1. A
graph with nine vertices
is the smallest possible
for Z3.
|
For
Z4,
again one
starts with a
square, but as
before there
are extra
rotations.
The smallest
graph this
time turns out
to have 10
vertices.
(A 12-vertex
graph
analogous to
the 9-vertex
graph for Z3
does
have group Z4,
but a smaller
one
exists.)
Unfortunately,
this graph is
difficult to
draw in the
plane, and its
symmetries are
not easily
visible if so
drawn.
Thus we
exhibit this
graph in other
more pleasing
settings.
The graph has
vertices 1, 2,
3, 4, 1', 2',
3', 4', 1'',
2'' and the
symmetry group
(isomorphic to
Z4
) is
G
= { (1), g,
g2,
g3}
where g
=
(1234)(1'2'3'4')(1''2'')
so g2
= (13)(24)(1'3')(2'4')(1'')(2'')
and g3
=
(1432)(1'4'3'2')(1''2'').
Figure 2 shows
an animation
of one such
arrangement;
visual
symmetry is
not clear.
 Figure
2.
Natural
minimal spatial
arrangement for the
cyclic group of order 4;
notice the lack of
visual symmetry
portrayed in this
correct representation
of this symmetric group. Figure
2.
Natural
minimal spatial
arrangement for the
cyclic group of order 4;
notice the lack of
visual symmetry
portrayed in this
correct representation
of this symmetric group.
|
Figure 3
improves
on Figure 2;
it displays
visual
symmetry.
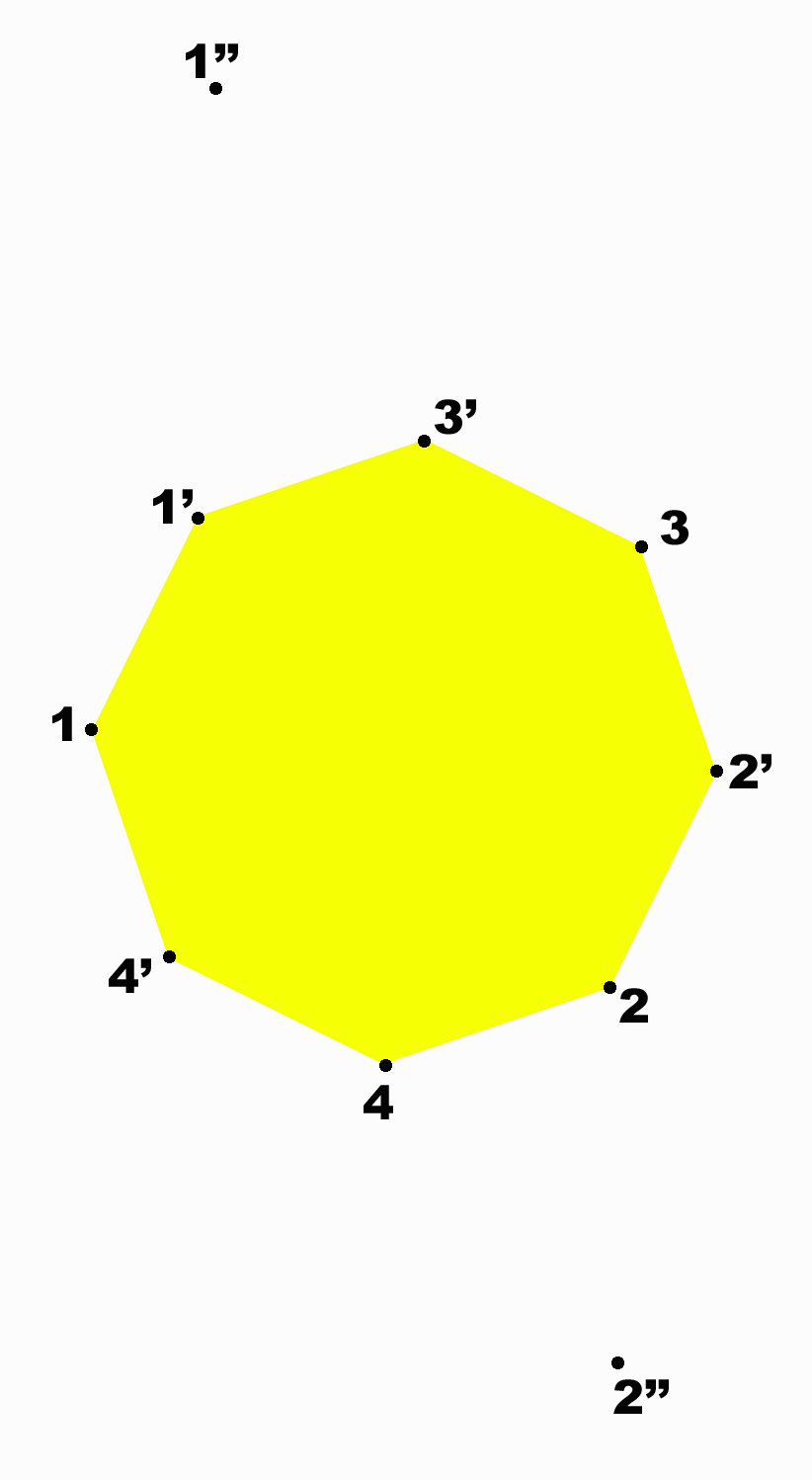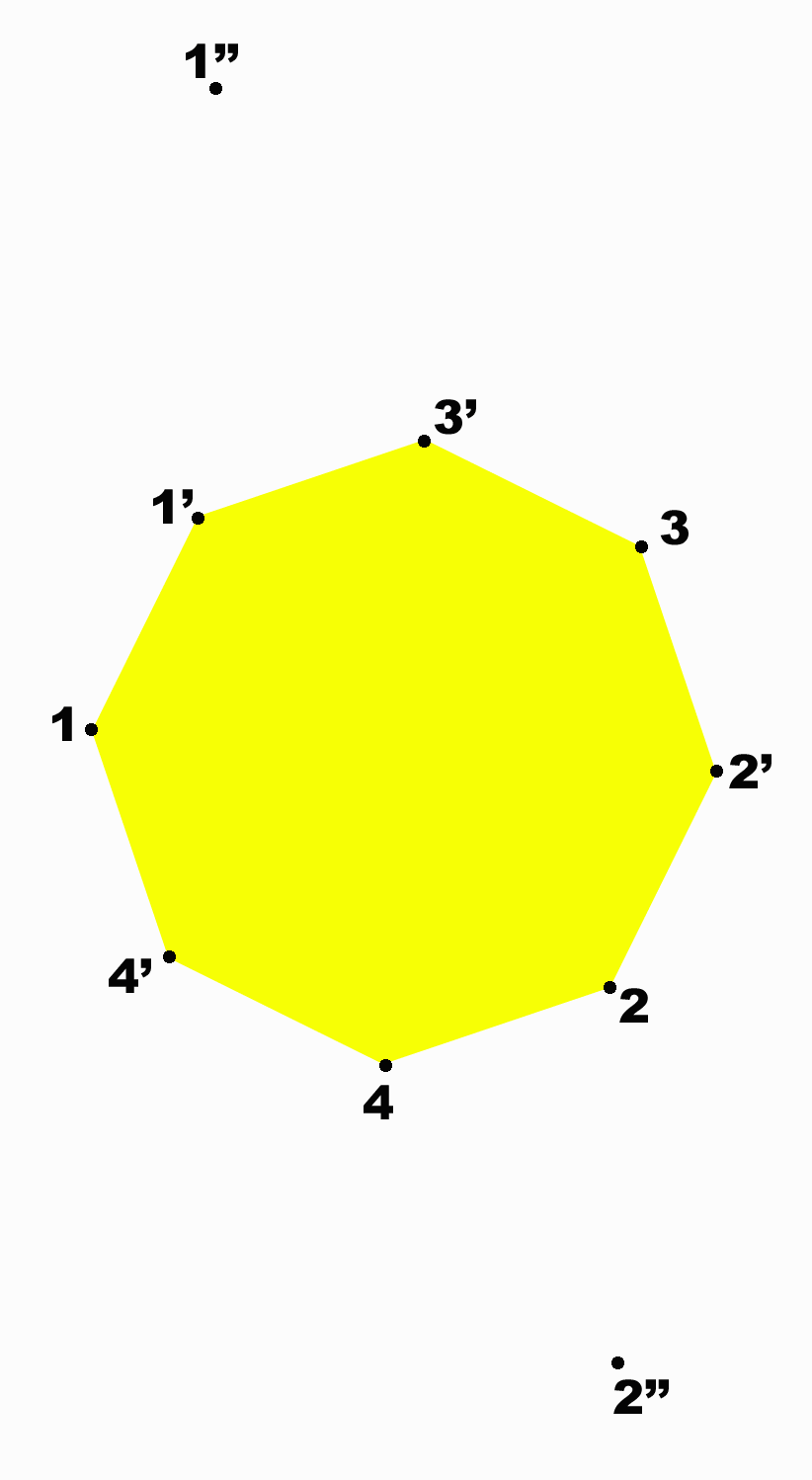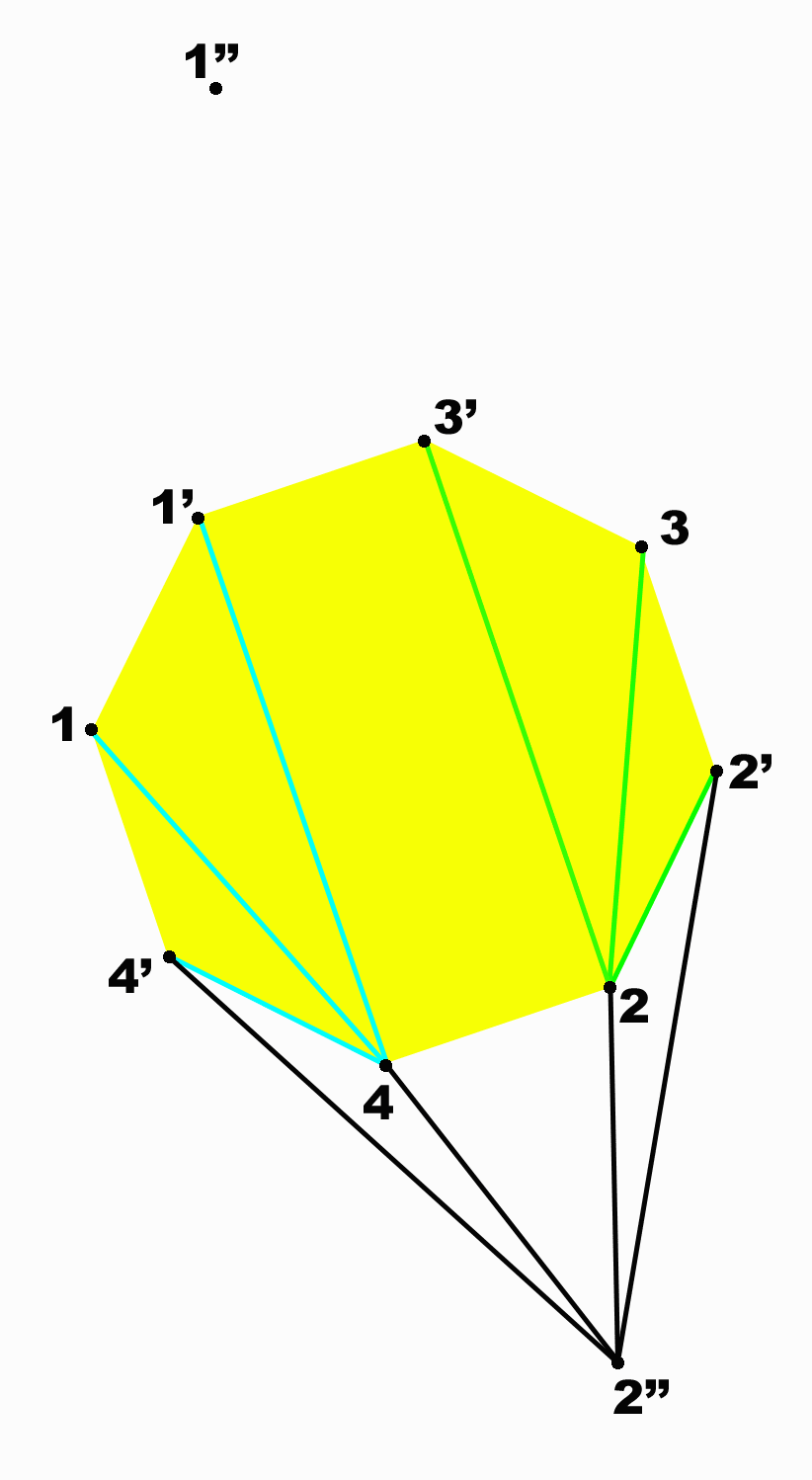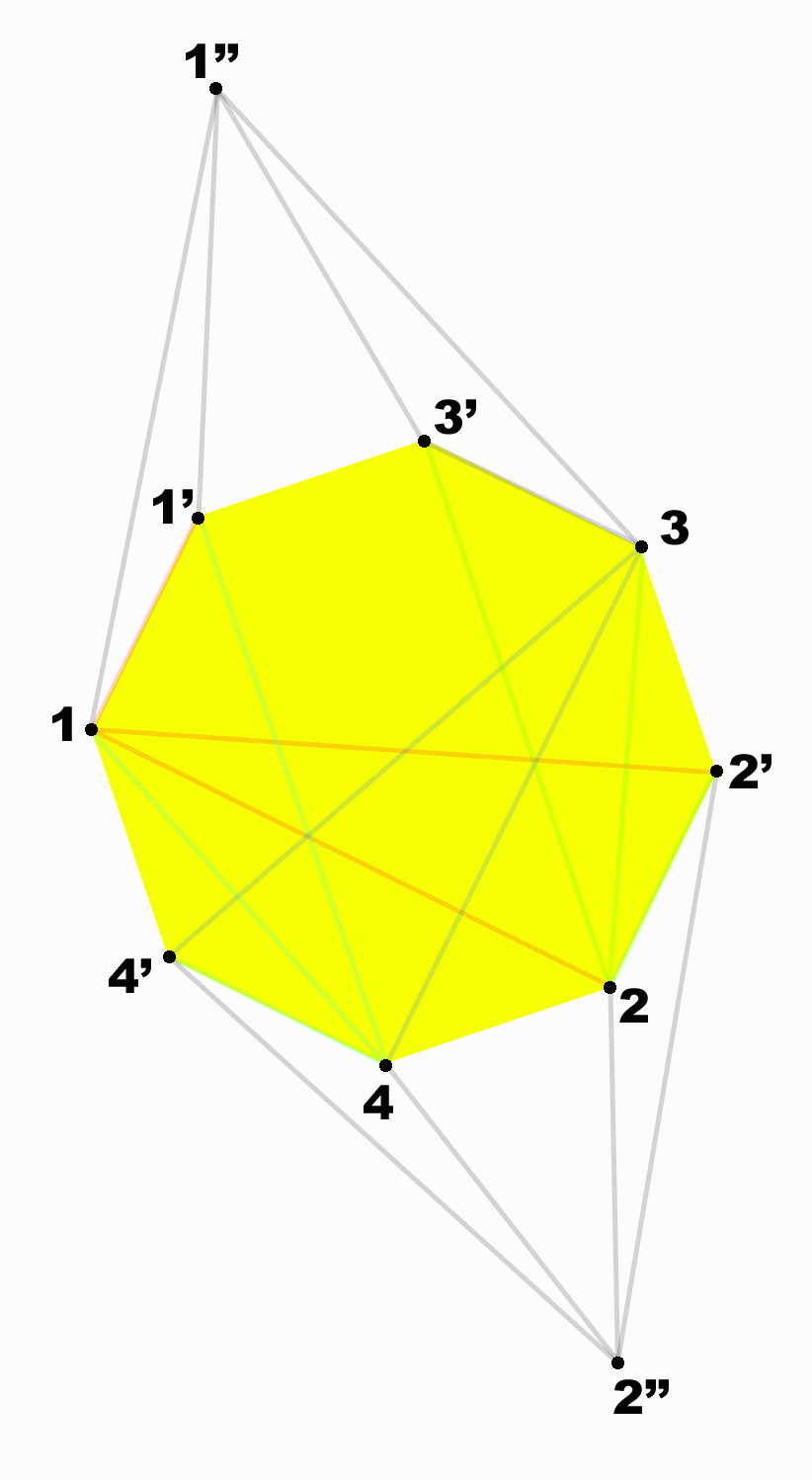
Figure 3.
Symmetry
displayed
spatially. Note
the position of 1, 2, 3,
4--it is similar in
spatial style to the
right-hand side of
Figure 1.
|
Figure
4
shows the
final frame of
the animation,
as a static
view of the
symmetric
spatial
arrangement.
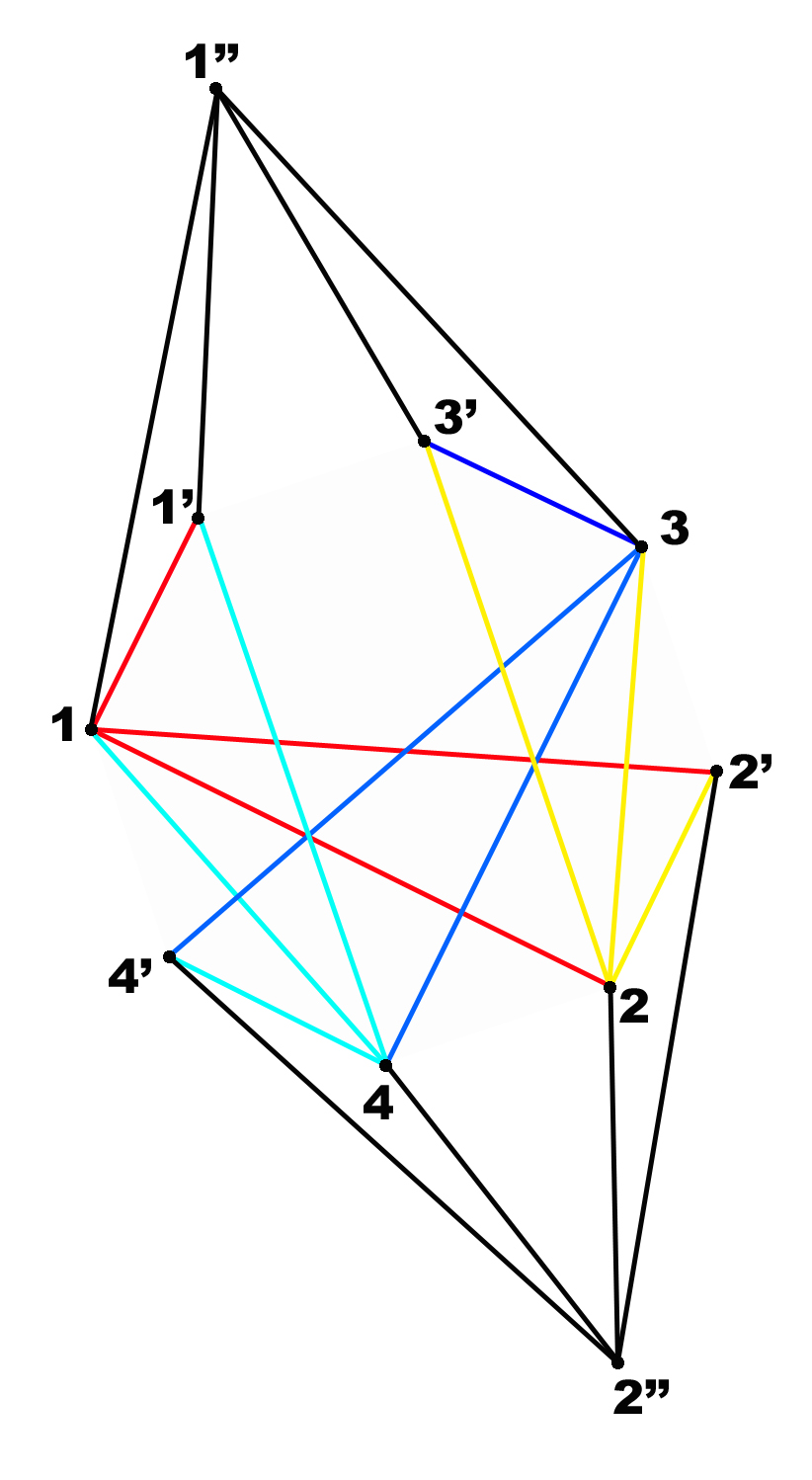
Figure 4.
Static
view of the final
frame of Figure 4.
|
As may often be the case,
geometric
views that become complex can
be improved, in terms of
comprehension, with
animation. Older texts might be
made to come alive (Harary,
1969); more recent ones can be
brightened (Arlinghaus,
Arlinghaus, and Harary,
2002; Arlinghaus and
Kerski (eBook version), 2013);
most important, animation can
do more than enhance existing
research--as it opens better
or new vistas, it can guide
it!
References
Arlinghaus, Sandra L. and
Kerski, Joseph.
2013. Spatial
Mathematics: Theory
and Practice through
Mapping. Boca
Raton: CRC Press.
Arlinghaus,
Sandra L.;
Arlinghaus, William C.;
and Harary, Frank.
2002. Graph
Theory and
Geography: An
Interactive View,
eBook. New
York: John
Wiley & Sons.
Arlinghaus,
William C. 1977.
The Classification
of Minimal Graphs with
Given Abelian
Automorphism
Group. Ph.D.
Dissertation, Department
of Mathematics,
Wayne State
University.
Arlinghaus,
William C.
1985. The
Classification of
Minimal
Graphs with Given
Abelian Automorphism
Group. Memoirs
of the American
Mathematical
Society
57(330).
Frucht,
Roberto.
1949.
Graphs of degree three with a given
abstract group. Canadian
Journal of
Mathematics
1 (4):
365-378.
Harary,
Frank. 1969.
Graph Theory.
Reading,
MA:
Addison-Wesley.
Wikipedia
Wolfram, Math World
|
In the In
|
|





 Figure
2.
Natural
minimal spatial
arrangement for the
cyclic group of order 4;
notice the lack of
visual symmetry
portrayed in this
correct representation
of this symmetric group.
Figure
2.
Natural
minimal spatial
arrangement for the
cyclic group of order 4;
notice the lack of
visual symmetry
portrayed in this
correct representation
of this symmetric group.